The Molniya orbitLet's start with something more involved and take a look at the Molniya orbit. This orbit is the solution to communication satellite problem of the former Soviet Union.Many communication satellites are placed in geosynchronous orbit where they remain stationary above a point on the Earth equator. However, for high latitudes, this is not optimal because such a satellite appears low in the sky. The solution to this was to place a satellite into a highly eccentric orbit such that it has its apoapsis at high latitudes. Since the orbital speed at the apoapsis of about 40.000 km is slow, this gives a window of several hours in which the satellite effectively remains stationary above a high-latitude spot on the ground. With three such satellites, continuous coverage can be achieved.
Setting up the orbitCreate the following config file (or copy it from the ones coming with the package):
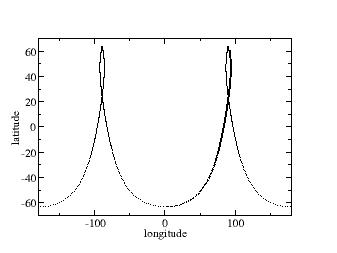
Let's discuss this a bit. An apsis of 40.000 km isn't exactly 'low orbit', so we need to change some defaults. First of all, the default time the software simulates forward is 5000 seconds- that's not enough. We use max_time to increase the window. However, that on its own won't do the trick - the max. number of points a plot can hold is 5000, the default timestep in the simulation is 0.01 s and a plot point is created every 100 timesteps or every second - so we would run out of points. Hence also the parameter plot2d_resolution is increased to write only every two-thousand timesteps (aka 20 seconds) - which gives enough room to look at two and a half orbits. In addition, we now set the gravity model to the most realistic model (J3) and Earth shape likewise to the realistic IERS ellipsoid. The position initializes the orbit at its perigee, and the speed is chosen from an analytical solution such that an apogee of 40.000 km is reached. Running this config file takes a bit (because the time interval is pretty large), but eventually you should be rewarded with this groundtrack:
As expected, the groundtrack slows down at high latitudes and eventually even goes eastward as part of the orbit has an apparent angular speed lower than Earth rotation before it bends westward again and completes a fast passage through the perigee.
Stability analysisIf you've been looking through the linked article on the orbit, you might have spotted the fact that the reason the peculiar inclination of 63.4 degrees is chosen for the orbit is that Earth's J2 gravity term does not drag the argument of the periapsis (and hence also the important location of the apogee) but leaves it stable at -90 degrees.Well, since we have a numerical tool, let's test this. Change the plot section to
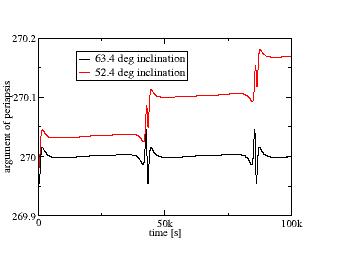
and re-run, then change the latitude in the position section to 53.4 degrees, assign a different filename and run again, then plot both - you should see this:
The argument of the periapsis is actually not constant in J3 gravity - this shouldn't be a surprise, because the gravity field affects different latitudes differently, so as the orbit changes latitudes, things deviate from perfect spherical gravity. But for 63.4 deg inclination the change is in fact periodic - the argument of the periapsis always comes back to the same angle. For 53.4 degrees, this is not the case, every orbit the parameter drifts by about 0.1 degrees, so over time a satellite placed into such an orbit will not longer have its apogee at high latitudes where it's needed - unless correction maneuvers are performed all the time. Make the test, switch gravity back to 'spherical' and you can verify that to a very good accuracy the argument of the periapsis does not change at all over the orbit as expected.
Continue with Properties of J2 and J3 gravity. Back to main index Back to science Back to LEO targeting Created by Thorsten Renk 2017 - see the disclaimer, privacy statement and contact information. |