Properties of J2 and J3 gravityThe terms J2 and J3 technically refer to an expansion of the gravity field of the planet into spherical harmonics (see e.g. the Geopotential Model). J2 and J3 are the dominant terms of this expansion.We've already mentioned that the J2 term parametrizes the equatorial 'bulge' of mass - as an even coefficient, it always has a north-south symmetry, i.e. in J2 gravity the bulge is the same north of the equator and south of it. The J3 coefficient however is odd, and hence it parametrizes the way gravity is different between northern and southern hemisphere. While the physics reason for the J2 bulge in terms of Earth rotation is fairly obvious, there is no equally compelling reason why there should be a J3 asymmetry. And because there is no such driving force, the J3 term is quite a bit smaller - we actually have to dig a bit to see it at all.
The role of J3Where to look for J3? We know that J2 for instance affects the eccentricity of the orbit - as we cross the equator on the ascending node and move to higher latitudes, there will be a force pulling us back towards the equator, and hence eccentricity will start to shrink. When we come back to the descending note, the opposite will happen, a small force will pull us faster to the equator as compared to the spherical case. Precisely the same will happen on the southern hemisphere. Thus, eccentricity variantions can be expected to be periodic.But now, if the pull is slightly equal when you come from the north or from the south, over time the variations will drift - and that we can try to observe. Create the following config file:
The orbital altitude is a bit low - but since we don't simulate atmosphere we can get away with it. Plot this, then change to J3 gravity and plot again. You should see something like this:
Now, this is a bit hard to spot, so there are some auxiliary lines added to the plot: The J2 gravity maxima and minima always come back to the same value and the variation is periodic, including the J3 terms this is no longer true - the solution drifts over time. Another instructive plot to make is eccentricity as a function of latitude - give it a try! But as expected, the J3 force is tiny as compared to the J2 perturbations (and you might already guess that any higher terms are even smaller still).
Drift in J2While perturbations to some orbital elements (such as the eccentricity) are periodic, others are no - in particular, the longitude of the ascending node, the argument of the periapsis and the mean anomaly can be shown to exhibit a drift over time of which the mean is given by:
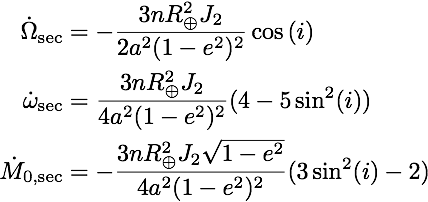
We've already seen an example of this in the Molniya orbit - if you look at the second equation, you can see that it happens to be zero when the sine term of the inclination just happens to cancel the constant in front - this determines the peculiar angle of 63.4 degrees. Now, let's look at the drift of the longitude of the ascending node instead. Change the plot section of the config file to
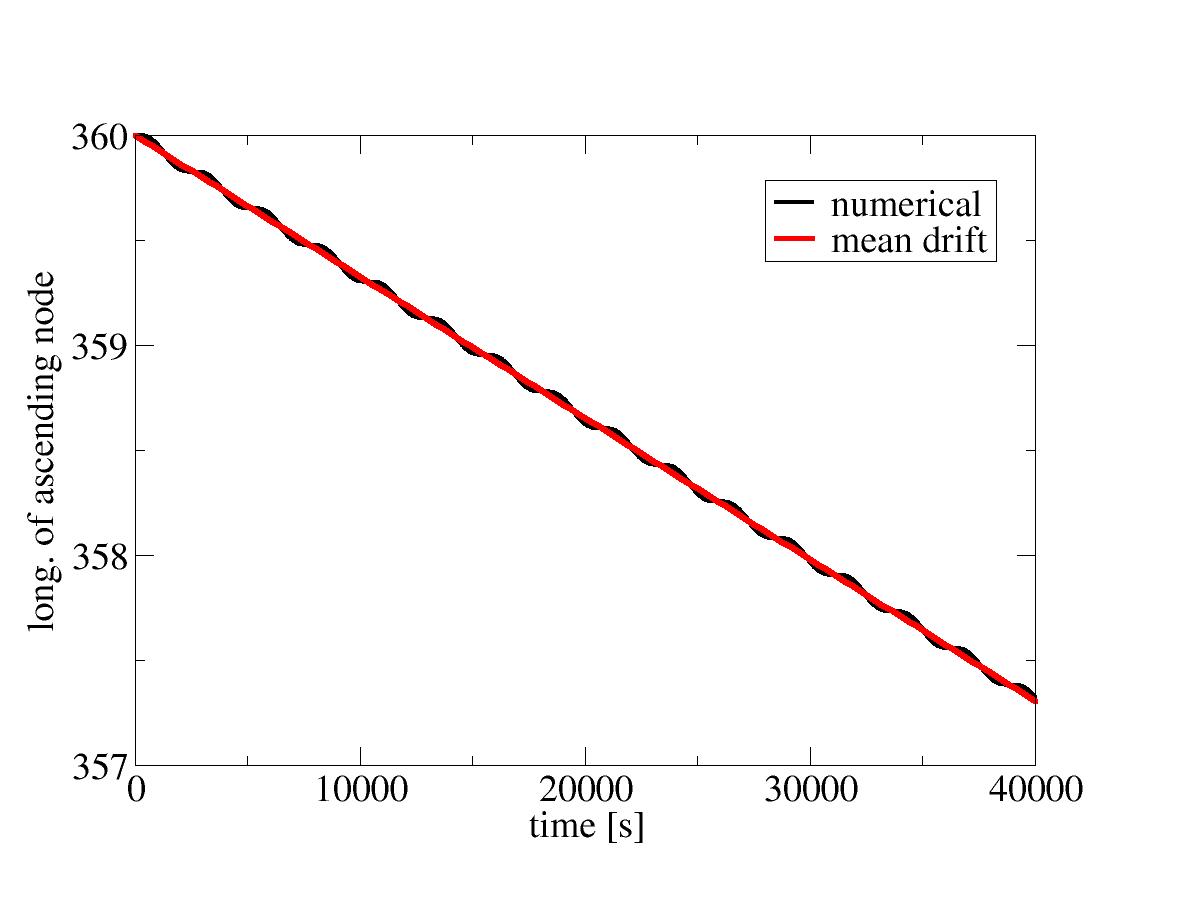
The result shows, as expected, a periodic variation on top of a constant drift.
Even over many orbits, the numerical solution is well followed by the analytical result, indicating that the code is stable and sufficiently accurate to capture J3 effects. Unlike the drift in the argument of the periapsis, this drift is present even for circular orbits and has implications for rendezvous maneuvers. From the plot, we can deduce that at 100 km altitude the ascending node drifts by a degree every three hours and 53 minutes. However, the drift dies out with altitude as the square of the Earth radius divided by the square of the semi-major axis - at 300 km altitude, it already is 6 percent slower. During the phasing period of a rendezvous, the chaser and target won't be at the same orbital altitude - and if they started out in the same plane, they won't be when the phasing is over due to this drift difference. This is important to keep in mind when planning.
Continue with Hohmann transfer. Back to main index Back to science Back to LEO targeting Created by Thorsten Renk 2017 - see the disclaimer, privacy statement and contact information. |