MoonsApart from planets (which orbit around stars), interesting and potentially habitable worlds include also moons (which orbit around planets). Since Earth's moon seems to be rather unusual in terms of being unusually large for the size of the planet, likely the most interesting moons orbit gas giants. The Galilean moons of Jupiter - Io, Europa, Ganymede and Callisto - are examples for such worlds.Especially if the moon is orbiting close to a giant planet (which to a degree all of the Galilean moons do), several effects are important: First, the moon may be tidally locked to its planet, i.e. orbit such that always the same hemisphere points towards the planet. For planets orbiting a star, tidal locking is rather dramatic as only one hemisphere of the planet receives light at all, for a moon the consequences are less drastic as in the course of an orbit around the planet, the light from the central star still reaches the whole surface. Except this isn't quite true because of eclipses - the planet-ward facing hemisphere is always likely to see the star eclipsed by the planet when local noon would occur. On the other hand, dependent on its albedo, the planet itself reflects light, and dependent on its temperature, it emits heat in the infrared. Both effects would tend to warm the moon on its planet-ward facing hemisphere and at least mitigate the effect of an eclipse. To take all of this into account, a moon is always simulated together with a planet on the same level of detail, i.e. if you want an irradiation model for individual surface elements, this needs to be done for both planet and moon.
A look at IoCreate the following configuration file:
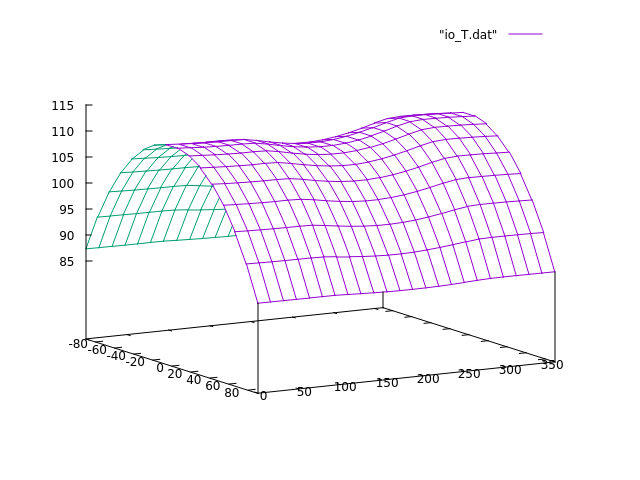
Most should be pretty self-explanatory, in essence the declaration of a moon uses the same keywords as for a planet with the orbital parameters being defined with respect to the planet. Generally close-orbiting moons require a low orbital simulation timestep to lead to numerically stable results, so even if the system simulates okay with a large timestep before adding the moon, this may no longer be the case afterwards. A fast-orbiting moon like Io will produce a flurry of eclipses, so the eclipse finder output can be long - eclipse_verbose false suppresses the output if desired. The keyword indirect_radiation determines whether the moon should receive reflected and infrared radiation from the planet - comparing this set to true or false allows to determine the strength of such effects. If you're interested in plotting the orbit, the key phrases body moon and relative_to planet may be helpful - the first tracks the orbit of the moon which by default is plotted around the system barycenter, the second sets the origin to the planet which gives the expected circular orbit. Finally, the keyword max_depth is crucially important for tidally locked worlds. We've discussed earlier that the simulation assumes that the thickness of the thermally active grows with the square root of the length of the day. However, for a tidally locked world, the length of the day is infinite (or at least really large in the simulation) - so it is not the relevant scale at which temperatures vary - in the case of Io, that is rather the 'year', aka the orbit around Jupiter. In such cases, the keyword allows to override the automatically determined value and prevent thermal inertia from growing unnaturally large. Running the file, you should get this result:
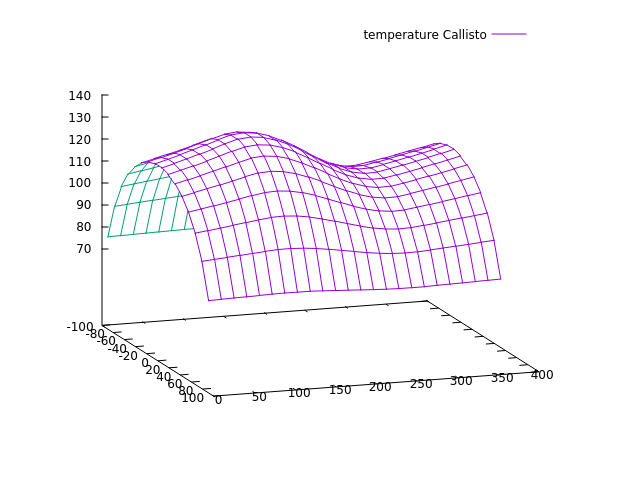
The distribution in latitude is given by the sun angle, the overall range agrees with measured values, the dip in mid-longitudes (the planet-facing side) is driven by eclipses (you can verify that by switching eclipse finder off, and also that the depth of the dip is a bit reduced by indirect radiation. But why is the distribution so flat in longitude, why is no solar heating peak seen? The apparent sun position moves around with the orbital period but Io's orbital period is just 1.7 days, so that is a fairly long 'day' and not a fast rotation that would flatten everything. It turns out however that in the temperature regime we're looking at here, this is a fast rotation. We've often been looking at worlds with the potential for liquid water, around 250 K. At the 100 K of Io, the Stefan-Boltzmann law states that the rate at which the surface cools is 40 times less than at 250 K. Also the solar irradiation is rather weak. As a consequence, compared with the timescales for cooling and heating, Io's rotation is blazingly fast, and hence there is no time to create a pronounced heating peak. A look at CallistoTo test this idea, let's replace Io by Callisto - which as an orbital period of 16.6 days.
We're getting the expected heating peak, and the somewhat remarkable result that Callisto is a bit warmer than Io, in spite of not having volcanic activity and a large internal heat flux:
Also, as expected, for an orbit so far from Jupiter, eclipses or indirect radiation do not play any significant role for the temperature evolution.
Continue with Measuring days. Back to main index Back to science Back to worldbuilder Created by Thorsten Renk 2021 - see the disclaimer, privacy statement and contact information. |