Rendezvous targetingSo far we've dealt with a variety of orbits and ways of changing from one into another. A rendezvous problem where one aims at reaching the position of another spacecraft is yet a different situation, because in this situation it matters when a certain point is reached - it is not sufficient to reach the same orbit as the rendezvous target, one also has to reach it when the target is actually there.In the following, we'll speak of the object we want to rendezvous with (be it a space station, a satellite or another spacecraft) as the target and the spacecraft we're maneuvering as the chaser, and we'll assume that only the chaser executes maneuvers whereas the target remains in whatever orbit it is and is only subject to whatever the orbital perturbations at that point are. The minimal number of burns to get the chaser to the target if their orbits are not already intersecting is two - we need at least one burn to get to get to the target position, but there the velocity will be different, so unless we do a second burn to match velocities at the intercept point, we'll drift away from the target again. Dependent on circumstances, it might be easier to do more than one burn.
Setting up orbital targetsLet's start with a simple situation - we'll set the chaser some 35 km behind the target into the same orbit and have a look at how to get there. The syntax for defining the initial target state is practically the same as for spacecraft, only instead of the keys state_vector or position rather the keys target_state_vector or target_position have to be used.Start a config file with the following lines to set up the desired situation:
Relative motion plotsIntuitively, we might have the idea that the target is really 'ahead' of us, and since we're in the same orbit it actually is not in any way 'left' or 'right' or 'above' or 'below'. In fact, if it'd be a large space station, we could likely already see it ahead. So such a coordinate system seems useful to decide what maneuvers to do.We can define a curved coordinate set which has the required properties. First, we can call the difference in radius vectors (defined from the center of Earth) the relative altitude or our z-coordinate. Now, if we would bring the chaser to the target altitude, we could go forward on the current orbit till we get to the closest approach to the target - this curved pathlength (the 'along-track' distance) can be the x-coordinate. Finally, the distance to the target at the point of closest approach (the 'cross-track' distance) is a good y-coordinate (with the positive direction defined by the cross product of x and z). These coordinates can be accessed once a rendezvous target is defined using the keywords target_prox_x, target_sprox_y and target_prox_z (the 'prox' stands for 'proximity' because the coordinate system is mostly useful close to the target - when chaser and target are in completely different orbits, they don't convey much information). If we're in the same orbital plane as the target, the cross-track distance is zero, so the y-coordinate is not interesting, and we can visualize what happens during a rendezvous by plotting the others via:
Doing the plot for the situation above, we find that the chaser remains at a constant distance of about 35 km behind the target - which is not surprising, because they're in the same orbit. So - how to do get there?
Fast transfersWell, it's only 35 km and we're in a rocket, so let's just light the thrusters for a bit and simply fly there! Let's program a prograde burn - and when we reach the target, we can do a retrograde burn to brake, and we're there. Something like
should get us to a decent intercept. Well, no - if you plot it, we're not actually getting anywhere close to the intercept point. The prograde burn moves us indeed forward a tad, but the increased centrifugal force moves us upward, that slows us down, so what we actually do is climb to an apsis of 35 km above the target and gradually fall behind. What if we burn harder - and add a downward radial component into the fray? Well, using the relative motion plot to target the trajectory, we might reach the zero point (and hence a rendezvous) with something like
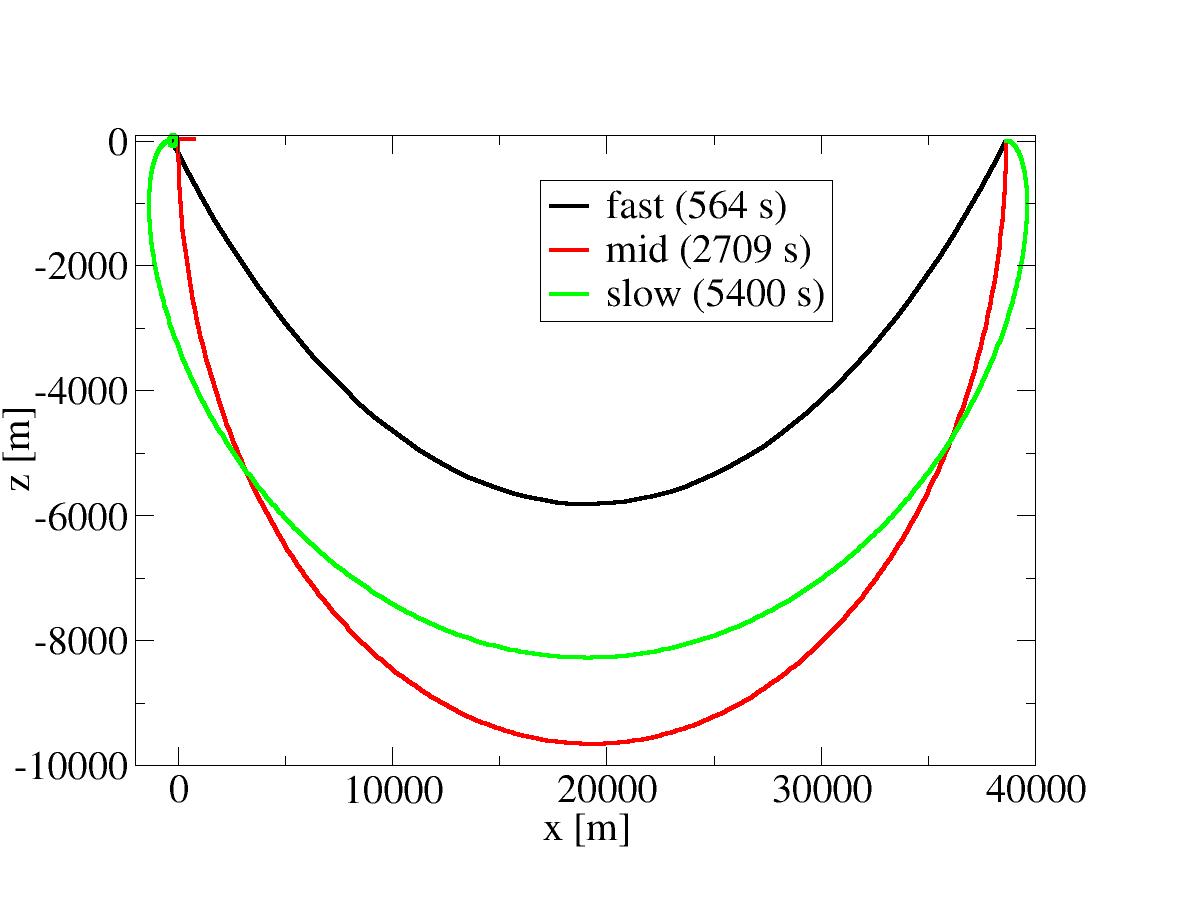
it turns out we can actually make it in a bit over nine minutes - problem solved. Except, looking at the numbers and considering the propellant needs, this solution has ridiculously large requirements. The delta v requirements are those of a major orbit change - yet we just want to move 30 km forward. Let's try something different.
Mid-length transfersThe reason the simple prograde burn did not result in good transfer was centrifugal force - it made the chaser go up, and then due to energy conservation it had to slow down. So can't that effect be used instead - we can maneuver the chaser down, and energy conservation will make it faster, so we'll catch up with the target (and eventually centrifugal force will push us up to it again)?Let's try a small radial downward burn. We'll get to see an ellipse in the relative motion plot that reaches closer to the target. By changing the amount of radial burn, we can make the ellipse intersect the zero point, and if we take out the vertical motion at that point, we're right at the target position. If you've played around with this correctly, you should end up with about
So that looks better - we need about half an orbit to transfer, and the velocity requirements are not quite as insane. Can we do it yet cheaper?
PhasingThe theme of the last section has been that going lower means orbiting faster, hence we can catch up. But in fact we'll catch up on any orbit that has a somehwat lower orbital period. Since the orbital period is a function of the semi-major axis only, by suitable changing the semi-major axis to a lower value we can in fact dial the catch-up rate to any value we like. This technique is known as phasing. So any retrograde burn will reduce the orbital period and mean we catch up with the target. Such a burn will also mean that the burn point establishes an apoapsis and a periapsis 180 degrees from it. Thus, to meet up with the target, the catch-up rate needs to be arranged such that we encounter the target at the apoapsis (when we have the z-coordinate zeroed).We can do that by starting with very small retrograde burns and plot the result. The relative motion plot will show a line rolling downward, then forward and coming up to zero altitude. What needs to be done is to adjust the strength of the burn such that one of the vertical zeros also falls onto a horizontal zero. If the first peak is adjusted, we find something like
but in principle there's also yet cheaper solutions which reach the target after two, three or many orbits. So among all transfer solutions we've studied here, phasing is the cheapest, but also the most time-consuming. For comparison, take a look at all the trajectories in the same relative motion plot - they look surprisingly similar!
Now, what would be useful is an ability to find a solution corresponding to a desired transfer time automatically. This is known as 'Lambert's Problem' in orbital mechanics, and we'll study it next.
Continue with The Lambert problem. Back to main index Back to science Back to LEO targeting Created by Thorsten Renk 2019 - see the disclaimer, privacy statement and contact information. |