Ion thruster insertionWe've seen in the last tutorial that a geosynchronous insertion is relatively propellant-demanding. The reason for this is of course the relatively low specific impulse a liquid rocket engine delivers - if an ion thruster would be used, the specific impulse could be a lot higher, leading to a much reduced propellant consumption.The down-side of this is of course that the thrust such engines can realistically deliver is a lot lower than for liquid rocket engines. It is in fact so low that one can not assume the validity of the impulse approximation at all - the burn time to deliver the needed delta v is larger than the orbital period. It follows that one can not simply keep thrusters ignited to achieve e.g. circularization, because if the engine burns for a whole orbit, both apoapsis and periapsis are increased and circularization never happens. Instead, the engine needs to be periodically ignited once the spacecraft is close to the point where the burn would have to be done in the impulse approximation (the details of 'close' depend on the accuracy that needs to be reached). Thus, over the course of many periods, the orbit is gradually deformed in the desired way. Let's study a model for such an insertion.
Spacecraft and burn targetingWe want to re-do the geosynchronous insertion of the last tutorial using an ion thruster. Since this is going to take a long time, we need to set the plot resolutions to larger timeskip values - and at the same time we might increase the timestep of the simulation and trade some accuracy against a faster result.
The satellite itself also has the same mass, but instead a 3 N ion thruster and much less propellant
We could program a long series of PEG-7 burns to define when the thruster is supposed to ignite, but this would be awkward - instead, we can define a condition when this is supposed to happen. This is done by specifying a target vector and a tolerance - whenever the normalized velocity vector (aka the prograde unit vector) dotted into the target vector gives a number larger than the tolerance, the thruster comes on. If we make the target vector agree with the prograde unit vector at the apoapsis, we'll always ignite the thruster around the apoapsis to circularize. There is of course a catch when we change orbital plane - then also the prograde unit vector at the apsis changes. However, the code automatically forces the target vector to lie in the current orbital plane, so as the plane is changed, the condition also changes (since this is done anyway, we don't even need to take care that the input vector is normalized or in the plane). The following section describes such a burn condition - with a tolerance of 0.8, the angle may be off by about 35 degrees, so the condition is fairly permissive and the thruster will fire over a long arc.
If you run the resulting burn and plot e.g. inclination vs. time, you'll see that the burn fails to null inclination, and even adding further normal delta v won't help. Also, if you plot the trajectory, you'll see that not only the periapsis is raised, but also the apoapsis grows a bit. Both are the result of the permissive tolerance - we might tighten it, then we get more accurate results, but it will take longer to achieve the desired final orbit.
Refining the orbitOn the other hand, we might simply correct the error by adding burns with tighter limits.
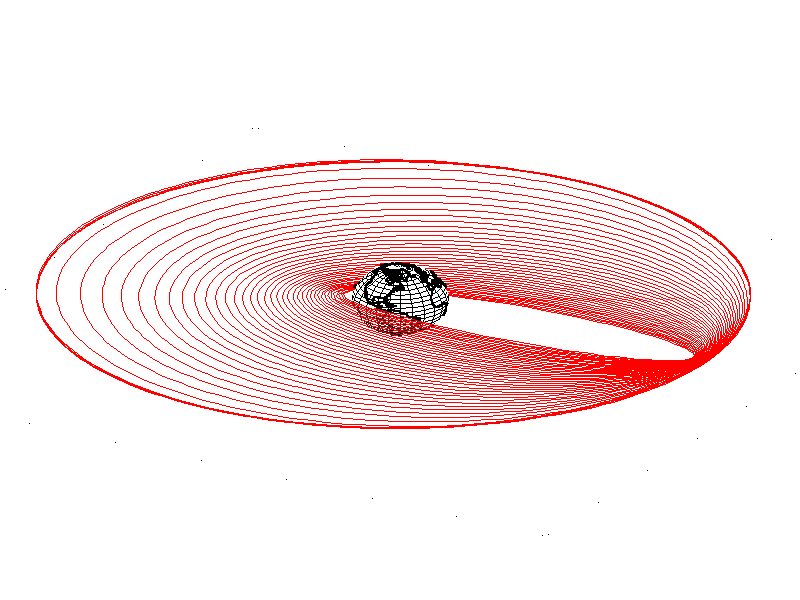
These burns need to be done at 90 degrees with each previous one, because that's where the inclination error accumulates. Using these two correction, inclination can be very efficiently nulled. The 3d trajectory, when plotted, results in an intricate manifold where the initial elliptic and finite inclination orbit is gradually circularized and moved into the equatorial plane.
The transfer made this way is much longer, but also much more propellant-efficient. You can play with the value of the tolerance to see how this prolongs the insertion time while taming the growth of the apogee. Also, plotting the value of the inclination over time is interesting to see what part of the orbit the thruster is on.
Continue with Orbiting the Moon. Back to main index Back to science Back to LEO targeting Created by Thorsten Renk 2018 - see the disclaimer, privacy statement and contact information. |