Shuttle insertionDuring the early Shuttle era, the mission profile of the Space Shuttle involved a main-engine cutoff (MECO) not quite at orbital speed such that when the external tank was separated, it would fall right back into the atmosphere. Instead, the OMS engines were used to push the Shuttle first to an apsis at the altitude of the desired orbit during the OMS-1 burn, and then the engines were ignited again at the apsis for circularizing the orbit during the OMS-2 burn.While not yet in a stable orbit, the Shuttle avionics is in the so-called operational sequence OPS 1 and nominally uses PEG-4 targets for both burns. Let's investigate this situation. Shuttle peculiaritiesThere's a few technicalities we need to take care of now. First, the Shuttle is not targeted in SI units but in imperial units, so we need to switch the unit system to be able to input in miles and feet. Second, ignition times for burns are specified in mission-elapsed time (MET) - if we want to program burns for the Shuttle, we need this format. Also, we need to tell the simulation at which point in time we'd like to start since the LEO targeting software can't do interaction with the atmosphere, we can not simulate the ascent phase itself.Also, in OPS 1 the Shuttle has a bit of a peculiar way of defining ThetaT targets - they're not measured from the ignition point of the burn but from the launch site. As a result, we need to tell the program where the launch (and landing) sites are. Finally, if the ascent itself is done by a different software (in this case Flightgear), we can directly copy the state vector information (3-component inertial position and velocity vectors) to the targeting software.
The insertion programTo do all of this, create the following config file (where a launch from a completely fictional site at (0,0) longitude and latitude has been done to obtain the state vector).
Let's look at what this does. The config section switches to imperial units and MET time format, but for the time being we still use spherical gravity and Earth shape. The situation we pick up is 10 minutes past liftoff (as given by the MET string) i.e. a few minutes past MECO and the external tank is separated. At this point, we are in fact not in a circular orbit but on a rising trajectory (you can verify this by plotting the orbit without any burns) - with a periapsis inside the atmosphere. The first burn instructs to place an apsis at an altitude of 185 miles with a transfer angle of 170 degrees from the launch site (if we were at the periapsis, this would be 180 degrees, but we are in fact not), to be started 30 seconds after the simulation began. The second burn takes place at the expected time of the periapsis and instructs the solver to look for an apsis 340 degrees from the launch site (i.e. almost opposite to the insertion point). You may wonder where the ignition time and thetaT values come from (H and c1 = c2 = 0 are perhaps easier to guess). In the event, they're taken from NASA documents and close to what STS-30 used. Let's run the files.
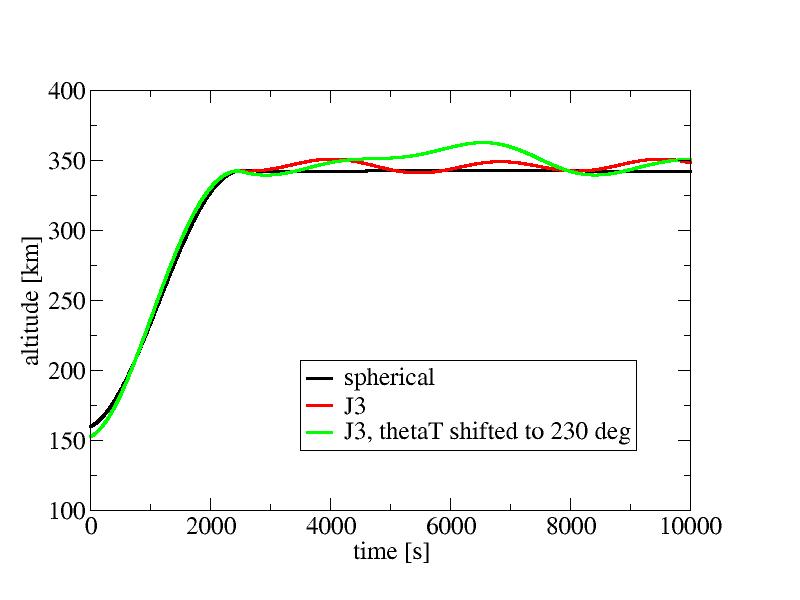
Targeting in J3 gravityThe fit runs for a small bit, and you may note that it spits out ignition times in MET format rather than seconds, ready to go into the Shuttle avionics.If you plot the result, it looks pretty much as expected - a nice insertion into a circular orbit. Now, let's get realistic and switch gravity to J3 and shape to IERS and re-do the program. Not nearly as nice - what happened?
Well, first of all you may note that the altitude even at the beginning is quite a bit lower - that's the equatorial bulge of the planet adding a good 10 km of solid ground underneath. And as we fly to higher latitudes, it gradually goes away. That's in addition to the J2 terms of the potential pulling less at higher latitudes. Under these conditions, it's in fact impossible to fly a constant-altitude orbit, no matter how good the targeting software is. It simply can't be done. So how good is out solution then? Let's for instance change thetaT to 230 degrees - for the spherical case, this makes no real difference. The J3 case however changes a lot - in fact it looks worse. This illustrates one of the problems of targeting under realistic conditions - there are spurious 'apses' created by the J2 perturbations- maxima and minima along the trajectory which the fit can key on, but which are usually not what we want to target. This is the reason we program the second target almost 180 degrees from the ignition point - we know that in the spherical case the periapsis will be there, and that the J2 terms are symmetric there, and if we target that point, we'll get as clear from spurious results as it gets.
OptimizationIf you look through the burn parameters, you'll notice that both burns have a sizable radial component - the OMS-1 comes with 38.96 ft/s and a total burn duration of 154.84 s, the OMS-2 has -14.9 ft/s radial component and needs 119.19 seconds. Could we perhaps do better?Remember what the radial components in the fit do - they correct a 'wrong' placement of the apses relative to the target. But there's other ways of influencing this. For instance, we could shift ignition time, then we'd reach the apsis later. Or use a different transfer angle target. It depends a bit on what we want. For the first burn, we'd like to do it early and we'd like to reach the target apsis - the transfer angle isn't really that crucial. The second burn on the other hand we'd like to target at the nominal periapsis to get a good circularization, but we could live with shifting ignition time to get the optimal placement of the burn right at the apsis. This is the kind of targeting mission control needs to do, and in fact we can do it. Add
to the first burn and
to the second burn - this allows to change target angle (ignition time) if there's a scenario with a lower radial component available. (As a side note, if time is optimized, the nominal ignition time sets the lower part of the search window the fit explores, so if the fit does not converge, the reason might be that it would like to lower TIG but can in fact not because the window is too narrow). Re-run the scenario. The result almost looks like the nominal insertion, but we make do with near-zero radial components and 154.72 s of burn duration fo OMS-1 and 116.91 s for OMS-2. We just saved 2.4 seconds burn time (a bit less than a percent of propellant). Perhaps not staggering - but interesting to see that we can get an optimum that way. With the last solution, we've in fact come a long way from the analytical Hohmann result and are now fully in the realm of numerical orbit optimization - despite all complications of finite burn duration, J3 gravity and non-circular initial orbit, we still get an optimized burn solution delivered for any halfway reasonable targets.
Continue with Shuttle deorbit burn. Back to main index Back to science Back to LEO targeting Created by Thorsten Renk 2017 - see the disclaimer, privacy statement and contact information. |