Structure of GanymedeBackgroundThe visible surface of a planet is often shaped by processes that happen in the interior. A hot interior can pile up mountain ranges via plate tectonics or volcanism for instance, a thin crust can lead to large-scale flooding of surface features by liquid material from below and volcanism is often a source for atmosphere gases.The aim of the geology module is to estimate the effect of such processes. The basic idea is that once the composition of a world is specified - in the case of the Jupiter moon Ganymede for instance a iron-sulfide core surrounded by a layer of silicate rock and an outer layer of water ice, this information can be used together with the overall density to compute the layer boundaries (taking into account the density increase due to compression - for instance iron at the Earth's core has a ~50% higher density than on the surface). From there, the various sources of heat can be assessed, leading to a prediction for the internal heat flow at the surface. Once that is known, the simulation can compute inwards to compute the internal pressure and temperature, using phase information about the various materials to determine thermal conductivity (or convective transport coefficients). In this way, parameters like the crust thickness and the presence of a liquid or solid core can be assessed. From these, tentative estimates as to what elevation differences the surface of the body can show can be made. It should be evident that uncertainties are as a rule large since even for Earth the interior is not precisely known, as no in-situ measurements are possible and various coefficients of materials at pressures exceeding a few million bar are not readily accessible. For instance the primordial heat component radiated by Earth is estimated to be 5-15 TW - with that kind of uncertainty, one cannot expect precise answers.
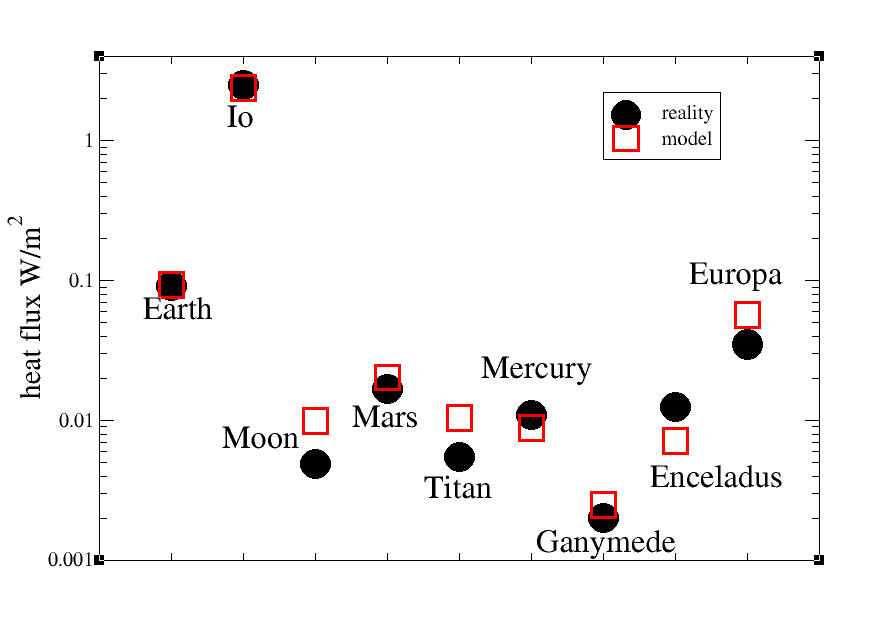
Heat fluxThe interior of a world can be hot due toa) primordial heat: This is thermal energy left over from the formation of the planet. Since radiation from a heat reservoir is a surface to volume problem, primordial heat is usually only present in young, large and massive worlds. The simulation assumes that primordial heat is concentrated towards the center of the body. b) radiogenic heat: This component comes from the decay of radioactive substances mainly embedded into silicate rock. The relevant isotopes are 232Th, 238U, 40K and 235U. Since the amount of these elements decreases over time, radiogenic heating is also large for younger worlds. The simulation assumes that radiogenic heat is produces in silicate rock or carbon layers with a bias towards the lower part of the layer. c) tidal heat: The friction when the shape of a body responds to tidal effects on an eccentric orbit also can be a significant cause for heating, especially for moons orbiting giant planets or planets orbiting very close to stars. This mechanism is most effective for massive central bodies and close-byeccentric orbits. The actual amount of heating crucially depends on the amount of internal friction which converts the distortions into heat, and the simulation assumes that tidal heating is most prominent towards the surface where distortions are largest. Using what is known for the composition of a selection of solar system bodies and evaluating the different heat sources leads the following comparison between predicted and what is known of measured heat fluxes:
This is generally not too bad - usually predictions differ no more than a factor two from reality, despite covering a pretty large range of 0.002 - 2.5 W/m^2. The results could be improved by using e.g. the information that for formation of bodies farther from the star, the concentration of heavy elements is reduced.
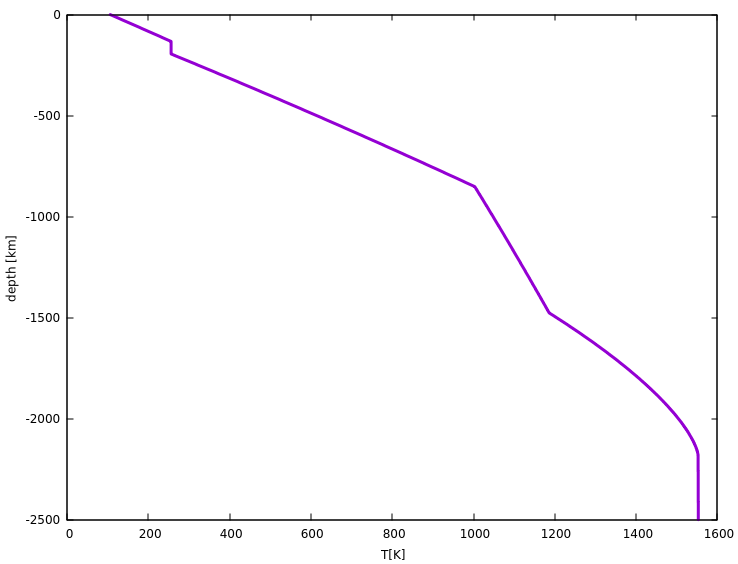
Temperature gradientsHeat fluxes require a temperature gradient, if the thermal conductivity of a material is known, the gradient can be computed from the flux and the conductivity, and so the simulation can assess how temperature rises when one goes deeper into a body. The pressure in the depths can simply be evaluated by computing the gravitational force exerted by all the column above. Knowing temperature and pressure, phase diagrams can be used to determine whether a material reaches e.g. a melting point.When this happens, usually thermal conductivity is no longer the relevant parameter, as convective transport can happen - the material itself moves and transports heat with it. For a liquid such as water, this happens near instantaneous when compared with geological timescales. For silicate rock, the material actually becomes 'fluid enough' to enable solid convection which moves material with speeds of centimeters per year - and still this is vastly more efficient than heat conduction. Parameters for convective transport in the simulation are obtained from what is known about thermal gradients in Earth's mantle. Calculating inward from the surface finds the following thermal profile for Ganymede:
Initially heat conduction in solid ice transports thermal energy, then a liquid subsurface ocean is reached and temperature remains constant for some depth interval, then the different phases of high-density ice become relevant until at a depth of ~800 km silicate rock is reached and then, finally the core.
Detailed information, surface morphologyRunning a detailed profile reveals that the simulation results in a subsurface ocean of liquid water beneath a layer of ice at a depth of 172 km. Below that ocean continue the high-density phases ice VI and ice VII (both heavier than water) till the solid silicate rock and core are reached.How high could mountain ranges be on Ganymede? One can evaluate two limiting factors. One of them is isostasy - since the crust is floating on top of liquid, piling material on top of the crust would push it down. Eventually that would mean that the material pushed into the liquid would melt and hence the pile above would sink. The thicker the crust above the liquid, the higher elevations could be. Isostasy allows higher elevations for a silicate rock crust floating on lava (as there can be substantial density differences between crust and mantle rock) and less for water ice (the density difference between liquid water and ice is comparatively small, ice sinks deep in water). Another limit is posed by erosion - a comparison of erosion rates on Earth shows that geologically stable terrain features erode rather slow (5-10 m per million years) whereas rising mountain ranges like the Himalayas erode much faster (600+ m per million years) - quite independent of climate or other conditions. Gravity playes a huge part here, because while chemical weathering, thermal weathering or micrometeorites can all shatter rock, only gravity can transport the debris away, so low gravity would tend to allow much higher mountain ranges than high gravity. Combining the limits, the simulation states that Ganymede could have 8 km tall mountain ranges - quite tall for an ice world, but then again smaller Iapetus has a 20 km tall ridge. In actual reality, Ganymede does not have mountains coming close to the limit though.
Config fileThe complete definition of Ganymede, its orbital and thermal properties and its geology is as follows:
Back to main index Back to science Back to worldbuilder Created by Thorsten Renk 2024 - see the disclaimer and contact information. |